Вращение многозвенной цепи


Примером многозвенной цепи является манипулятор робота. Другим примером может являться собственно робот, выполненный в виде змееподобного организма. Еще более сложный пример - это вращение нуклеотида в цепи РНК (см. проект RNAInSpace).
В таких случаях рассчитывать вращение отдельных звеньев цепи в одной системе координат нецелесообразно. Поэтому применяют относительное описание, когда положение каждого следующего звена описывается относительно предыдущего.
Однозначное описание положения тела в пространстве
[править]Чтобы однозначно задать положение твердого тела в пространстве, надо зафиксировать три его точки, не лежащие на одной прямой.
Степени свободы
[править]Одна материальная точка имеет три степени свободы (координаты x, y, z). Две материальные точки, жестко связанные между собой, имеют 3 + 3 - 1 = 5 степеней свободы. Одна степень свободы вычитается, так как координаты точек и не являются независимыми величинами, так как имеется одно уравнение связи. Три материальные точки, жестко связанные между собой, имеют 3 + 3 + 3 - 3 = 6 степеней свободы. При этом имеются три уравнения связи, выражающие постоянство расстояний между каждой парой точек.
Шесть степеней свободы тела описываются тремя координатами точки О (центр в системе ) и тремя углами однозначно определяющие положение системы относительно . Эти углы называются углами Эйлера (они будут рассмотрены позже).
Повороты
[править]
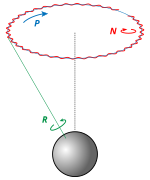
- Углы Эйлера — углы, описывающие поворот абсолютно твердого тела в трёхмерном евклидовом пространстве:







